По решению Ученого совета было выбрано 4 важнейших результата за 2024 год.
Авторы: д.ф.-м.н. Медведев С.Б.,к.ф.-м.н. Васева И.А., ак. РАН Федорук М.П
Нелинейное преобразование Фурье (НПФ) позволяет проинтегрировать нелинейное уравнение Шредингера (НУШ), получая при этом информацию о структуре сигнала и о наличии в нём солитонов. НУШ широко применяется, в частности, в задачах нелинейной волоконной оптики, поскольку описывает распространение импульсов в оптоволокне. Обобщением НУШ, учитывающим явление поляризации, является система уравнений Манакова. Реализация обратного НПФ является сложной математической проблемой, требующей решения системы интегральных уравнений с учётом экспоненциальных зависимостей в ядре. Разработка эффективных методов для реализации НПФ позволит осуществлять более реалистичные расчеты при построении телекоммуникационных систем передачи данных, основанных на солитонных сигналах. Такие системы позволят компенсировать нелинейные искажения сигнала и выйти за пределы ограничений линейных методов передачи данных. Сущность результата заключается в новом методе повышенного порядка точности для численной реализации обратного НПФ для НУШ и системы Манакова. Метод позволяет повысить точность решения задачи до шестого порядка, по сравнению с известными методами второго порядка. Предложенный алгоритм также является быстрым, поскольку сохраняет квадратичную вычислительную сложность.
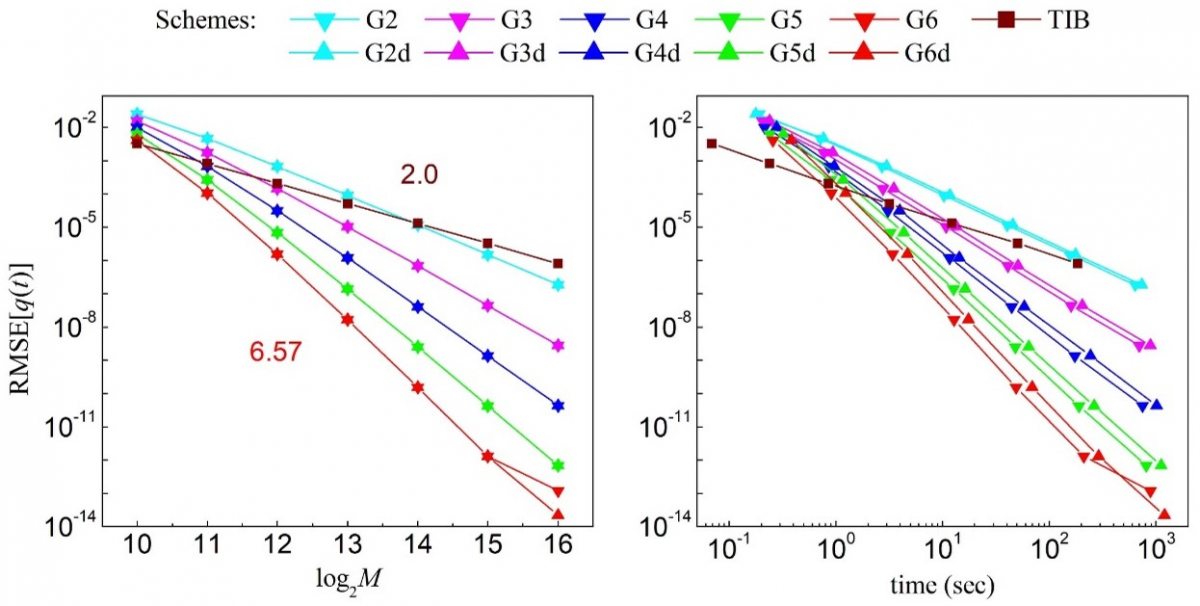
Сравнение численных схем для обратного НПФ на примере НУШ. Зависимость средне-квадратичной погрешности восстановления сигнала q(t) от числа точек M (слева) и от времени расчета (справа). Порядок аппроксимации известной схемы TIB – 2; новой схемы G6 – 6.57.
2. Безопасность России. Мониторинг, риски и безопасность Сибирского федерального округа. Кузбасс. Енисейская Сибирь. Байкал
Авторы: д.т.н. Москвичев В.В., д.т.н. Потапов В.П., д.т.н. Счастливцев Е.Л., ак. РАН Шокин Ю.И., д.т.н. Лепихин А.М., д.ф.-м.н. Чубаров Л.Б., к.ф.-м.н. Тасейко О.В., к.т.н. Постникова У.С., к.ф.-м.н. Пестунов И.А., к.т.н. Чернякова Н.А., к.т.н. Попов С.Е., к.т.н. Перетокин С.А., к.т.н. Кузьменко А.П., Короленко Д.Б., Короленко Л.А., к.т.н. Анискович Е.В., к.т.н. Доронин С.В., к.т.н. Харлампенков И.Е.
 В 2024 г. по решению Редакционного совета издательского проекта «Безопасность России. Правовые, социально-экономические и научно-технические аспекты» осуществлено издание 2-х томов, посвященных проблемам природно-техногенной безопасности Сибирского федерального округа.
В 2024 г. по решению Редакционного совета издательского проекта «Безопасность России. Правовые, социально-экономические и научно-технические аспекты» осуществлено издание 2-х томов, посвященных проблемам природно-техногенной безопасности Сибирского федерального округа.
Устойчивое социально-экономическое развитие территориальных образований связано с обеспечением национальной безопасности России и ее составляющих на региональном уровне. Обобщены результаты исследований в области комплексной безопасности субъектов СФО.
Монографии включают: характеристику органов управления безопасностью, технологий мониторинга; анализ рисков природных и техногенных ЧС с учетом особенностей СФО; результаты космического мониторинга; разработки информационных систем управления рисками; оценку состояния природно-техногенной, промышленной, энергетической, радиационной и сейсмической безопасности субъектов СФО, безопасности ГЭС, водопользования промышленных агломераций, бореальных лесов Сибири; оценку территориальных рисков развития и защищенности Кемеровской, Иркутской областей, Красноярского края с позиций концепции рисков развития социально-природно-техногенных систем; базовых и нормативных значений территориальных рисков с учетом промышленного развития (угледобывающие, нефтегазодобывающие, арктические территории, Байкальская природная территория).
Издание не имеет аналогов в отечественной практике. В работе приняли участие более 30 организаций, в т.ч. 18 институтов СО РАН, 6 ведущих вузов региона. Авторский коллектив включает 165 человек. Основная часть работы выполнена сотрудниками ФИЦ ИВТ.
3. Численное исследование закономерностей развития инфаркта миокарда, отягощенного многососудистым поражением коронарного русла
Авторы: д.ф.-м.н. Воропаева О.Ф., Цгоев Ч.А.
Завершен цикл исследований в области математического моделирования воспалительной фазы инфаркта миокарда. Получены следующие новые результаты:
- разработаны точечная математическая модель триггерного типа и соответствующая ей реакционно–диффузионная модель динамики некротической гибели сократительных клеток сердечной мышцы; реализованы в виде программного комплекса эффективные алгоритмы решения прямых (начальных для жесткой нелинейной системы ОДУ и начально-краевых) и обратных коэффициентных задач; выполнена калибровка моделей с привлечением широкого круга экспериментальных временных рядов и интегральных оценок, описывающих инфаркт миокарда в левом желудочке сердца мыши;
- исследованы сложные сценарии образования крупного очага повреждения, отягощенные неоднородностью свойств среды, иммунной реакции и ишемических повреждений миокарда;
- установлены базовые закономерности течения воспалительной фазы инфаркта:
- локализация области повреждения преимущественно в границах начальных очагов некроза в зонах, затронутых ишемией;
- тенденция к образованию крупного очага повреждения из нескольких соседствующих очагов некроза в зонах, затронутых ишемией, и его выраженная пространственно-временная неоднородность, обусловленная эффектом «памяти» об особенностях начальных (индивидуальных) условий;
- волновая природа воспалительной реакции и М1/М2 поляризация макрофагов как основной механизм формирования квазистационарных структур, ассоциированных с защитным демаркационным воспалением.
В рамках принятой модели показана высокая вероятность тяжелого течения или даже терминального сценария инфаркта при высокой интенсивности фоновой (на момент начала инфаркта) воспалительной реакции. На основании результатов вычислительных экспериментов сформулированы рекомендации для практической реализации оптимальных терапевтических противовоспалительных стратегий управления процессом функциональной поляризации макрофагов и/или цитокинами для снижения уровня повреждения миокарда, в том числе с учетом «терапевтического окна».
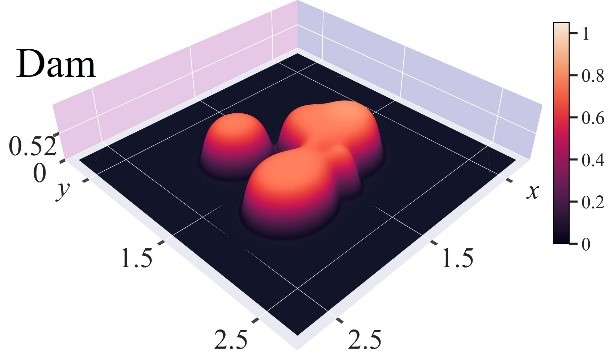
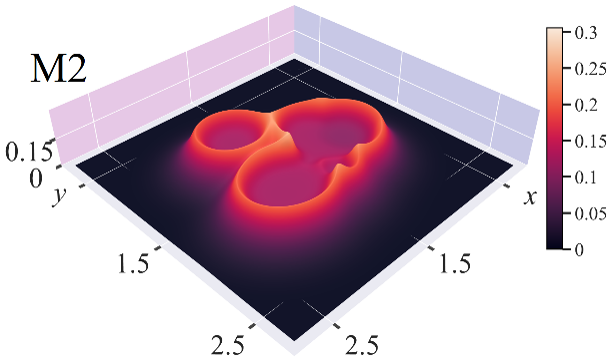
Иллюстрация зоны повреждения миокарда (а) и защитного демаркационного воспаления (б) при инфаркте в левом желудочке сердца мыши.
4. Новый метод построения помехоустойчивых кодов позволяющий улучшить границу Варшамова - Гильберта
Автор: д.т.н. Рябко Б. Я.
Коды, обнаруживающие и исправляющие ошибки, называемые также помехоустойчивыми, находят самое широкое применение в системах передачи и хранения информации и в значительной степени определяют развитие современных информационных технологий. В последние 70 лет разработкой и исследованием помехоустойчивых кодов заняты сотни ученых во всем мире, публикующих многочисленные монографии и статьи в десятках журналов.
Один из основополагающих результатов теории помехоустойчивых кодов, определяющий их предельные возможности исправления ошибок, получил название «граница Варшамова – Гильберта» (его открыли советский ученый Ром Рубенович Варшамов и американский Edgar Gilbert в 50-ые годы прошлого века).
В своей работе Рябко Б.Я. предложил основанный на линейных хеш-функциях новый метод построения помехоустойчивых кодов и успешно применил его к решению ряда важных задач обнаружения и исправления ошибок в системах хранения и передачи информации. В частности, предложенный им метод впервые позволил улучшить границу Варшамова – Гильберта.
Изображение:



